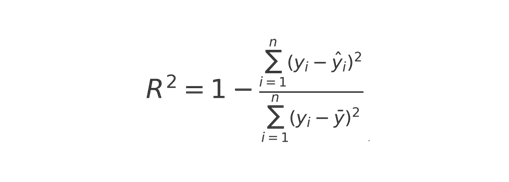Árvore de Decisão

Árvores de Decisão: Classificação e Regressão

As árvores de decisão são algoritmos de aprendizado supervisionado que podem ser usados tanto para classificação quanto para regressão. Elas funcionam de maneira hierárquica, dividindo os dados em subconjuntos com base em critérios que maximizam a separação entre as classes ou valores previstos. Cada divisão nos dados resulta em um nó na árvore, e os nós folhas representam as predições finais.

Como Funciona uma Árvore de Decisão

O algoritmo cria uma árvore binária que divide os dados com base em perguntas de “sim ou não” (ou condições que podem ser numéricas ou categóricas). O objetivo é dividir os dados de forma que, ao final, cada subconjunto tenha uma maior homogeneidade possível, ou seja, que pertençam a uma mesma classe (para classificação) ou que os valores sejam o mais próximos possível (para regressão).

Classificação

No caso de classificação, o objetivo é separar os dados em grupos distintos com base nas classes disponíveis. Por exemplo, ao classificar se um e-mail é “spam” ou “não spam”, a árvore de decisão usará características do e-mail (tamanho, palavras-chave, etc.) para fazer divisões sucessivas até chegar a uma classificação final.

Regressão

Já na regressão, o algoritmo tenta prever um valor numérico contínuo. Por exemplo, podemos prever o preço de uma casa com base em suas características (tamanho, localização, etc.). A árvore de decisão dividirá o conjunto de dados para minimizar a diferença entre o valor real e o valor previsto.

Construção da Árvore de Decisão

O processo de construção da árvore envolve o seguinte:

1. Seleção do Melhor Atributo: Para cada nó, o algoritmo seleciona o melhor atributo para dividir os dados. O critério de escolha varia entre classificação e regressão.

2. Cálculo da Impureza ou Erro:

   • Na classificação, o algoritmo calcula a impureza de um nó usando métricas como a Entropia ou o Índice de Gini.
   • Na regressão, ele tenta minimizar o Erro Quadrático Médio (MSE) ou outro erro associado à variância dos dados.

3. Divisão Recursiva: O processo é repetido recursivamente até que os dados estejam completamente separados ou até atingir um critério de parada, como uma profundidade máxima da árvore ou um número mínimo de amostras por nó.

4. Poda: Para evitar o overfitting (quando o modelo se ajusta demais aos dados de treino e perde capacidade de generalização), pode-se utilizar métodos de poda. A poda reduz o tamanho da árvore cortando nós que não agregam valor à predição.

Métricas de Avaliação

Para Classificação:

• Acurácia: Proporção de predições corretas sobre o total de predições.

• Precisão: Proporção de verdadeiros positivos sobre o total de predições positivas feitas pelo modelo.

• Revocação (Recall): Proporção de verdadeiros positivos em relação ao total de exemplos que realmente pertencem àquela classe.

• F1-Score: Média harmônica entre a precisão e a revocação. É útil quando há um desbalanceamento nas classes.

Para Regressão:

• Erro Médio Absoluto (MAE): Média das diferenças absolutas entre os valores preditos e os valores reais.

• Erro Quadrático Médio (MSE): Média das diferenças quadráticas entre os valores preditos e os valores reais.

• R-quadrado ( \(R^2 \)): Medida que indica o quão bem os valores preditos se ajustam aos valores reais.

O Parâmetro ccp_alpha (Poda de Custo Complexo)

O parâmetro ccp_alpha é usado para controlar a poda de custo complexo em uma árvore de decisão. A poda é essencial para reduzir o overfitting em árvores muito profundas. O ccp_alpha permite especificar um valor de regularização que penaliza a complexidade da árvore, ou seja, árvores mais simples (com menos nós) são preferidas se o aumento de precisão for pequeno.

A fórmula usada para calcular a penalidade é dada por:

Onde:

• \(R(T) \) é o erro da árvore \(T\).
• \(alpha \) é o parâmetro de regularização (ccp_alpha).
• \(\left|T\right|\) é o número de nós na árvore.

Quanto maior o valor de ccp_alpha, mais agressiva será a poda da árvore. Com um valor ccp_alpha = 0, a árvore será a mais complexa possível.

Exemplo Prático em Python

Aqui está um exemplo de como usar árvores de decisão para classificação e regressão, e como aplicar a poda com o parâmetro ccp_alpha:

Classificação

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score

# Carregar dados
dados = load_iris()
X_train, X_test, y_train, y_test = train_test_split(dados.data, dados.target, test_size=0.2, random_state=42)

# Criar o modelo
modelo = DecisionTreeClassifier(random_state=42)

# Treinar a árvore de decisão
modelo.fit(X_train, y_train)

# Fazer predições
y_pred = modelo.predict(X_test)

# Avaliar o modelo
acuracia = accuracy_score(y_test, y_pred)
print(f"Acurácia: {acuracia:.2f}")

# Aplicando a poda
path = modelo.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

# Treinando com poda
modelo_podado = DecisionTreeClassifier(random_state=42, ccp_alpha=ccp_alphas[-1])
modelo_podado.fit(X_train, y_train)

y_pred_podado = modelo_podado.predict(X_test)
acuracia_podada = accuracy_score(y_test, y_pred_podado)
print(f"Acurácia após poda: {acuracia_podada:.2f}")

Regressão

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

# Carregar dados
dados = load_boston()
X_train, X_test, y_train, y_test = train_test_split(dados.data, dados.target, test_size=0.2, random_state=42)

# Criar o modelo
modelo = DecisionTreeRegressor(random_state=42)

# Treinar o modelo
modelo.fit(X_train, y_train)

# Fazer predições
y_pred = modelo.predict(X_test)

# Avaliar o modelo
mse = mean_squared_error(y_test, y_pred)
print(f"MSE: {mse:.2f}")

# Aplicando a poda
path = modelo.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

# Treinando com poda
modelo_podado = DecisionTreeRegressor(random_state=42, ccp_alpha=ccp_alphas[-1])
modelo_podado.fit(X_train, y_train)

y_pred_podado = modelo_podado.predict(X_test)
mse_podado = mean_squared_error(y_test, y_pred_podado)
print(f"MSE após poda: {mse_podado:.2f}")

Casos de Uso

Classificação:

• Diagnóstico Médico: Determinar se um paciente tem uma doença com base em sintomas e exames laboratoriais.
• Detecção de Fraude: Identificar se uma transação bancária é fraudulenta ou não.

Regressão:

• Previsão de Preço de Imóveis: Estimar o preço de uma casa com base em sua localização, tamanho e características.
• Previsão de Demanda: Prever a quantidade de produtos que será vendida em um determinado período.

Conclusão

As árvores de decisão são ferramentas poderosas tanto para classificação quanto para regressão. Embora fáceis de interpretar, sua flexibilidade pode levar ao overfitting. O uso do parâmetro ccp_alpha é fundamental para aplicar poda e melhorar a generalização do modelo.